Notice
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
Tags
- 파이썬 텍스트 변환 #파이썬 공부
- PDF 개행문자
- 파이썬 음성인식
- 파이썬 유튜브
- 통계 #ROC #TPR #FPR #TNR #이진분류 #Accuracy #Recall
- 파이썬 채팅
- 파이썬 엑셀 파일 읽고 쓰기
- 파파고 꿀팁
- 리눅스#모의해킹#리눅스명령어#head 명령어
- 파이썬 #
- 파이선 행
- 파이썬 음성파일 텍스트 변환
- 파이썬#파이썬경로#파이썬폴더#파이썬디렉토리
- 파이썬 #파이썬프로젝트 #파이썬 예시 #파이썬 파일경로 #파이썬 자동화
- ROS #Robotics #ROS기초
- 스트림 암호 one-time-pad 공격#보안#암호
- 파이썬 예시
- 논문번역 꿀팁
- 패스트 캠퍼스 #자율주행 #비전
- 파파고 번역
- 파이썬 파일 전송
- ROS #spin() #spinOnce() #ROS기초
- 크롬오류#크롬검색어자동완성끄기#검색어자동완성오류#검색어자동완성 제거#검색어 노란선#검색어반복입력
- 리눅스기초#리눅스명령어#리눅스 tail#tail#모의해킹 리눅스
- 파이썬#subprocess#communicate()
- pdf 번역
- 파이썬 프로젝트
- QGC#QGrouncControl#GLIB오류
- 파이썬
- 파이썬 열
Recent Comments
Archives
개발자비행일지
Determinant of Matrix(행렬식의 정의) 본문
행렬식의 정의
행렬식(determinant)은 행렬을 대표하는 값으로 n x n (n은 2 이상)의 정사각행렬 A에 대해 다음과 같이 정의됩니다. detA11이란 A에서 1행과 1열을 제외한 행렬의 행렬식을 의미한다.
2 x 2 행렬의 요소값이 a,b,c,d 즉, [[a,b],[c,d]]라고 할 때 행렬식은 ad−bc 가 된다. .
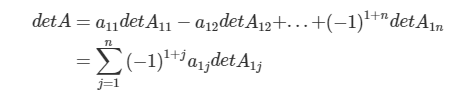
A가 다음과 같다고 할 때,
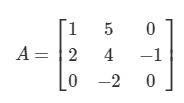
detA는 다음과 같이 계산된다. 아래에서 detAij는 A에서 i행j열을 소거한 행렬 값을 말한다.

지금까지는 행렬식을 구할 때 A의 첫번째 행을 쓰는 걸 기준으로 설명했지만, 행렬은 사실 어떤 행이나 열을 택하더라고 결국 행렬식은 같은 값이 나오는 성질을 가지고 있다. 이를 일반화 한 것을 Cij (i,j)-cofactor라고 한다.
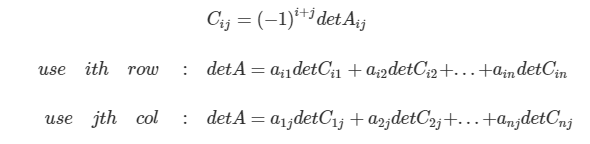
행렬식의 성질
행렬식의 성질은 다음과 같다.
(1) 행렬 A의 임의의 행에 스칼라 곱을 한 뒤 다른 행에 더해 BB를 만들었을 때 두 행렬의 행렬식은 같다.
(2) 행렬 A의 임의의 행을 다른 행과 바꾸어 B를 만들었을 때 detB=−detA
(3) 행렬 A의 임의의 행에 스칼라 곱을 해 BB를 만들었을 때 detB=kdetA
(4) 삼각행렬(triangular matrix)의 행렬식은 주 대각원소들의 곱과 같다.
(5) 행렬 AA가 가역(invertible)임과 detA≠0임은 동치.
(6) detAT=detA
(7) detAB=(detA)(detB)
'▶Theory' 카테고리의 다른 글
| 시상수 또는 시정수 (Time Constant) (0) | 2021.03.18 |
|---|---|
| Variance, Covariance 분산, 공분산 (0) | 2021.03.15 |
| Bayes Rule (베이즈 룰) (0) | 2021.03.15 |
| 테일러급수의 의미 (0) | 2021.03.15 |
| 행렬, 행 사다리꼴(Echelon form)이란 (0) | 2021.03.11 |




